

| [Home|Training|Problems|Contests|C Language] | [Login|Register] |
|
Problems Status Rank |
Problem 1026
Horse Shoe Scoring
Time Limit: 1000ms
Memory Limit: 65536kb Description
The game of horseshoes is played by tossing horseshoes at a post that
is driven into the ground. Four tosses generally make up a game. The scoring
of a toss depends on where the horseshoe lands with respect to the post.
If the center of the post is within the region bounded by the interior
of the horseshoe and the imaginary line connecting the two legs of the
horseshoe, and the post is not touching the horseshoe, it is a "ringer"
and worth five points. If any part of the horseshoe is touching the post,
it is a "toucher" and worth 2 points. If the toss is neither a ringer nor
a toucher and some part of the horseshoe will touch the post when it is
pivoted around its point B, it is a "swinger" and worth 1 point. Any horseshoe
which does not fit any of the scoring definitions scores zero points. See
the figures below for examples of each of the scoring possibilities. This program uses mathematical horseshoes that are semicircles with radius 10 centimeters. The location of the horseshoe is the given by two points: the centerpoint of the semicircle, measured in centimeters relative to x and y axes, and the point that exactly bisects the semicircle. The post is at location (0,0) and is 2 centimeters in diameter. The top of the post is level with the ground allowing the horseshoe to lay on top of the post; therefore, a "toucher" would mean that any part of the horseshoe lies within the circle with a radius of 1 centimeter centered at (0, 0). Each "turn" consists of four tosses. The purpose of your program is to determine the score of the "turn" by computing the sum of the point values for each of the four tosses. Input
Input to your program is a series of turns, and a turn consists of four
horseshoe positions. Each line of input consists of two coordinate pairs
representing the position of a toss. Each coordinate consists of a floating
point (X,Y) coordinate pair (-100.0 <= X, Y <= 100.0) with up to
3 digits of precision following the decimal point; the first and second
numbers are the X and Y coordinates of the centerpoint of the horseshoe
semicircle (Point A) and the third and fourth numbers are the X and Y coordinates
of the point (B) which bisects the horseshoe semicircle. You can be assured
that the distance between points A and B for each horseshoe will be exactly
10 centimeters. The figure below illustrates the meanings of the values
on each line.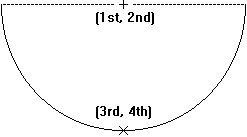 The first four lines of input define the horseshoe positions for the first turn; lines 5 through 8 define the second turn, etc. There are at most 999 turns in the input file, and every turn contains four horseshoe positions. Your program should continue reading input to the end of file. Output
The first line of output for your program should be the string "Turn
Score" in columns 1 through 10. For each "turn", your program should print
the number of the turn right-justified in columns 1-3 (turns are numbered
starting with 1), a single space (ASCII character 32 decimal) in columns
4 and 5, and the score for the turn right-justified in columns 6 and 7
with a single leading blank for scores 0 to 9. Numbers that are right-justified
should be preceded by blanks, not zeroes, as the fill character.
Sample Input
76.5 53.3 76.5 43.3 -5.1 1.0 4.9 1.0 5.1 0.7 5.1 -9.3 7.3 14.61 7.3 4.61 23.1 17.311 23.1 27.311 -23.1 17.311 -23.1 27.311 -23.1 -17.311 -23.11 -27.311 23.1 -17.311 23.1 -27.311 0.0 7.0 -6.0 -1.0 18.0 -24.0 9.0 -12.0 4.0 9.0 4.0 -1.0 -10.0 -13.0 -19.0 -25.0 Sample Output
Turn Score 1 10 2 0 3 7 |