

| [Home|Training|Problems|Contests|C Language] | [Login|Register] |
|
Problems Status Rank |
Problem 1134
Seats taking-up
Time Limit: 1000ms
Memory Limit: 65536kb Description
A as we all know, some students get up unbelievable early and take up many seats in the library. Other students (let’s call them normal students) often have problems taking up there, especially for those who are not single and want to sit next to his girlfriend (or her boyfriend).
The following assumption will be kind of exaggerating. Mr. Single gets up not that early, but he can always find a suitable seat in the library. Today he finds out that he is always the last single one there (pretty weird, Eh), then he wants to figured out that at most how many "GG&MM"s can take up their seats satisfactorily. This problem seems a little bit complicated for him. So he wants you to write a program to solve the problem. To simplify the problem, we assume the seats in the library form a n *m grid( n rows and m columns), and every cell in the grid represents a seat. Some students get up very early to take up a 1*1 grid for themselves. Mr. Single will always take up one after that. Then come the "GG&MM"s, they will always take a 1*2 grid or a 2*1 grid. No one will take a 1*1 grid after Mr. Single because he is always the last single one in the library. Your task is to tell Mr. Single, at most how many "GG&MM"s can take up their seats satisfactorily after his being there. Here is an example. The seats in the library form a 4 x 4 grid like this: (X stands for that the seat has been taken up.) 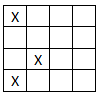
At most 6 "GG&MM"s can take up their seats in the library. For example they take seats like this: 
Input
The input consists a series data sets, followed by a final line containing 0 0 0.
There are 3 integers in the first line: m, n, k (0 < m, n <= 32, 0 <= K < m * n), the number of rows, column and the number of seats that have been taken up. In the next k lines, there is a pair of integers (x, y) in each line, which represents a seat in the x-th row, the r-th column that has been taken up. Output
For each problem instance, output at most how many "GG&MM"s can take up their seats satisfactorily.
Sample Input
4 4 3 1 1 3 2 4 1 0 0 0 Sample Output
6 |