

| [Home|Training|Problems|Contests|C Language] | [Login|Register] |
|
Problems Status Rank |
Problem 1237
Fake Problem
Time Limit: 1000ms
Memory Limit: 65536kb Description
Filix is an acm lover. Also he is an acm master-hand, because he can figure out the time complexity’s recursion of every acm problem. The recursion is given as T(n)=a*T(n/b)+f(n). In the recursion, n represents the scale of the acm problem, and the time complexity of f(n) is Θ(n^d). Regretfully, Filix cannot figure out the final time complexity by the recursion. Can you help him? Notice that Filix is not able to solve a Fake Problem. The acm problem is considered as a Fake Problem by Filix, only if the number a,b and d in the recursion satisfy the follow three requirements , (1)The number a fulfill the essential condition that number c=(2^a)+1 is a prime number; (2)The result of b*(b+1)/2 is both even number and perfect number. When the sum of all the factors of a number equals to the value of double itself, the number is called as perfect number. (3)The number d satisfies that: d=(c^b)%b。 Input
There are multiple input.For each input, there will be a Integer n(0<n<=10)in the first line,representing the test case num of the input. And ,for each test case, there will be three integers a, b and d (0<a<63,0<b<=1000000,0<=d<b) in one line. Output
For each test case, just output only one line. If the acm problem to be solved is a Fake Problem, then just output ”So sorry!”, indicating that Filix cannot solve this problem. Otherwise ,output three non-negative integers:x,y and z, indicating that the final time complexity is 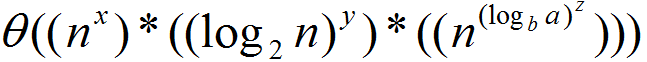 Sample Input
1 1 3 0 1 16 32769 57 Sample Output
0 1 0 So sorry! |