

| [Home|Training|Problems|Contests|C Language] | [Login|Register] |
|
Problems Status Rank |
Problem 1285
Oh my dear trees
Time Limit: 3000ms
Memory Limit: 65536kb Description
Given a weighted graph G with n vertices, G’s spanning tree is a connected subgraph of G which contains all vertices of G and exactly n−1 edges. The variance of a spanning tree T is defined as below: 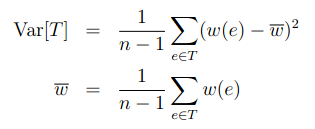
This problem requires you to find a spanning tree T with minimum variance. Input
The input contains multiple test cases. Each test case begins with a line containing two integers n and m, specifying the number of vertices and number of edges. Next m lines each contains three integers u, v and w, indicating there’s an edge between u and v weighted w. (1 ≤ u,v ≤ n ≤ 50, n−1 ≤ m ≤ 1000, 0 ≤ w ≤ 50) The input ends with n=m=0. It is guaranteed that the spanning tree always exists. Output
For each test case, output the minimum variance after “Case x: ”, where x is the case number. The answer should be rounded to 0.01. Sample Input
4 5 1 2 1 2 3 2 3 4 2 4 1 1 2 4 3 4 6 1 2 1 2 3 2 3 4 3 4 1 1 2 4 3 1 3 3 0 0 Sample Output
Case 1: 0.22 Case 2: 0.00 |