Given a weighted graph G with n vertices, G’s spanning tree is a connected subgraph of G which contains all vertices of G and exactly n−1 edges. The variance of a spanning tree T is defined as below: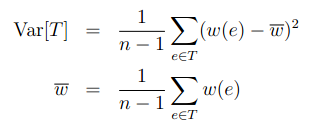

This problem requires you to find a spanning tree T with minimum variance.

The input contains multiple test cases. Each test case begins with a line containing two integers n and m, specifying the number of vertices and number of edges. Next m lines each contains three integers u, v and w, indicating there’s an edge between u and v weighted w. (1 ≤ u,v ≤ n ≤ 50, n−1 ≤ m ≤ 1000, 0 ≤ w ≤ 50)

The input ends with n=m=0.

It is guaranteed that the spanning tree always exists.

For each test case, output the minimum variance after “Case x: ”, where x is the case number. The answer should be rounded to 0.01.

4 5
1 2 1
2 3 2
3 4 2
4 1 1
2 4 3
4 6
1 2 1
2 3 2
3 4 3
4 1 1
2 4 3
1 3 3
0 0

Case 1: 0.22
Case 2: 0.00